一、基本概念
所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最优解。也就是说,不
从整体最优上加以考虑,它所做出的仅仅是在某种意义上的局部最优解。
贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择。必须注意的是,
贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备无后效性
(即某个状态以后的过程不会影响以前的状态,只与当前状态有关。)
所以,对所采用的贪心策略一定要仔细分析其是否满足无后效性。
二、贪心算法的基本思路
建立数学模型来描述问题
把求解的问题分成若干个子问题
对每个子问题求解,得到子问题的局部最优解
把子问题的解局部最优解合成原来问题的一个解
一、基本概念
所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最优解。也就是说,不
从整体最优上加以考虑,它所做出的仅仅是在某种意义上的局部最优解。
贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择。必须注意的是,
贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备无后效性
(即某个状态以后的过程不会影响以前的状态,只与当前状态有关。)
所以,对所采用的贪心策略一定要仔细分析其是否满足无后效性。
二、贪心算法的基本思路
建立数学模型来描述问题
把求解的问题分成若干个子问题
对每个子问题求解,得到子问题的局部最优解
把子问题的解局部最优解合成原来问题的一个解
三、该算法存在的问题
不能保证求得的最后解是最佳的
不能用来求最大值或最小值的问题
只能求满足某些约束条件的可行解的范围
四、贪心算法适用的问题
贪心策略适用的前提是:局部最优策略能导致产生全局最优解。
实际上,贪心算法适用的情况很少。一般对一个问题分析是否适用于贪心算法,可以先选择该问题下的几个实际数据进行分析,就可以做出判断。
五、贪心选择性质
所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择,换句话说,当考虑做何种选择的时候,我们只考虑对当前问题最佳的选择而不考虑子问题的结果。这是贪心算法可行的第一个基本要素。贪心算法以迭代的方式作出相继的贪心选择,每作一次贪心选择就将所求问题简化为规模更小的子问题。对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所作的贪心选择最终导致问题的整体最优解。
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用贪心算法求解的关键特征。
六、贪心算法的实现框架
从问题的某一初始解出发:
while (朝给定总目标前进一步)
{
利用可行的决策,求出可行解的一个解元素。
}
由所有解元素组合成问题的一个可行解;
七、题
1.背包问题
【背包问题】有一个背包,容量是M=150,有7个物品,物品可以分割成任意大小。要求尽可能让装入背包中的物品总价值最大,但不能超过总容量。
物品:A B C D E F G
重量:35 30 60 50 40 10 25
价值:10 40 30 50 35 40 30
分析:
目标函数: ∑pi最大
约束条件是装入的物品总质量不超过背包容量:∑wi<=M( M=150)
(1)根据贪心的策略,每次挑选价值最大的物品装入背包,得到的结果是否最优?
(2)每次挑选所占重量最小的物品装入是否能得到最优解?
(3)每次选取单位重量价值最大的物品,成为解本题的策略
值得注意的是,贪心算法并不是完全不可以使用,贪心策略一旦经过证明成立后,它就是一种高效的算法。比如,**求最小生成树的Prim算法和Kruskal算法都是漂亮的贪心算法。
贪心算法还是很常见的算法之一,这是由于它简单易行,构造贪心策略不是很困难。
可惜的是,它需要证明后才能真正运用到题目的算法中。
一般来说,贪心算法的证明围绕着:整个问题的最优解一定由在贪心策略中存在的子问题的最优解得来的。
对于例题中的3种贪心策略,都是无法成立(无法被证明)的,解释如下:
贪心策略:选取价值最大者。反例:
W=30
物品:A B C
重量:28 12 12
价值:30 20 20
根据策略,首先选取物品A,接下来就无法再选取了,可是,选取B、C则更好。
(2)贪心策略:选取重量最小。它的反例与第一种策略的反例差不多。
(3)贪心策略:选取单位重量价值最大的物品。反例:
W=30
物品:A B C
重量:28 20 10
价值:28 20 10
根据策略,三种物品单位重量价值一样,程序无法依据现有策略作出判断,如果选择A,则答案错误。但是果在条件中加一句当遇见单位价值相同的时候,优先装重量小的,这样的问题就可以解决.
所以需要说明的是,贪心算法可以与随机化算法一起使用,具体的例子就不再多举了。(因为这一类算法普及性不高,而且技术含量是非常高的,需要通过一些反例确定随机的对象是什么,随机程度如何,但也是不能保证完全正确,只能是极大的几率正确)。
假设我们有一个可以容纳 100kg 物品的背包,可以装各种物品。我们有以下 5 种豆子,每种豆子的总量和总价值都各不相同。为了让背包中所装物品的总价值最大,我们如何选择在背包中装哪些豆子?每种豆子又该装多少呢?

实际上,这个问题很简单,就是按照单价从大到小来装就行了,对吧?
以上本质上借助的就是贪心算法。结合这个例子,我总结一下贪心算法解决问题的步骤,我们一起来看看。
第一步,当我们看到这类问题的时候,首先要联想到贪心算法:针对一组数据,我们定义了限制值和期望值,希望从中选出几个数据,在满足限制值的情况下,期望值最大
类比到刚刚的例子,限制值就是重量不能超过 100kg,期望值就是物品的总价值。这组数据就是 5 种豆子。我们从中选出一部分,满足重量不超过 100kg,并且总价值最大。
第二步,我们尝试看下这个问题是否可以用贪心算法解决:每次选择当前情况下,在对限制值同等贡献量的情况下,对期望值贡献最大的数据。
类比到刚刚的例子,我们每次都从剩下的豆子里面,选择单价最高的,也就是重量相同的情况下,对价值贡献最大的豆子。
第三步,我们举几个例子看下贪心算法产生的结果是否是最优的。大部分情况下,举几个例子验证一下就可以了。严格地证明贪心算法的正确性,是非常复杂的,需要涉及比较多的数学推理。
实际上,用贪心算法解决问题的思路,并不总能给出最优解。
我来举一个例子。在一个有权图中,我们从顶点 S 开始,找一条到顶点 T 的最短路径(路径中边的权值和最小)。贪心算法的解决思路是,每次都选择一条跟当前顶点相连的权最小的边,直到找到顶点 T。按照这种思路,我们求出的最短路径是 S->A->E->T,路径长度是 1+4+4=9。
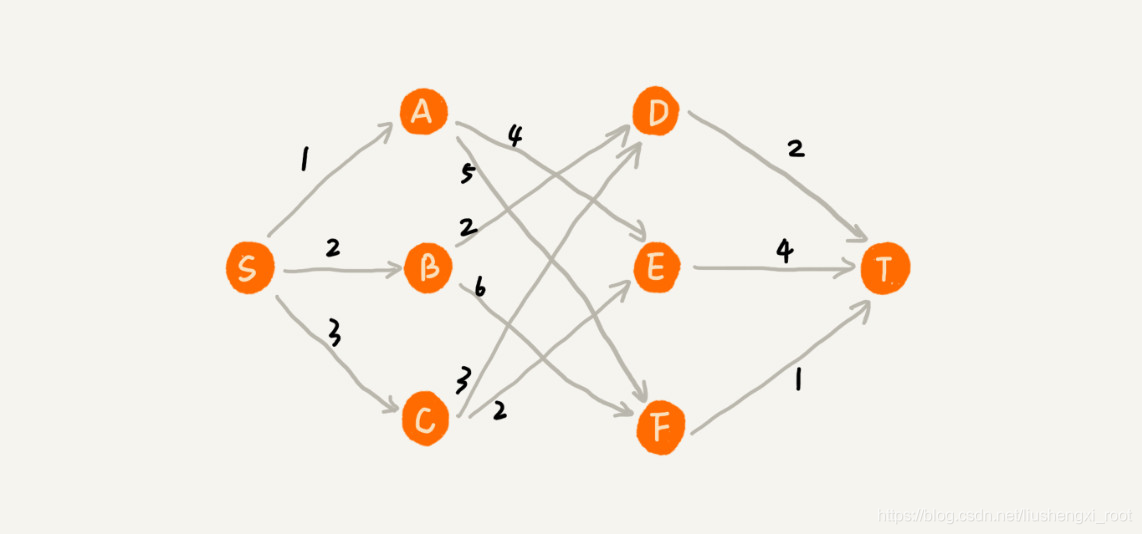
很明显,这不是最短路径,最短路径是S->B->D->T,那么这是为什么呐?
在这个问题上,贪心算法不工作的主要原因是,前面的选择,会影响后面的选择。如果我们第一步从顶点 S 走到顶点 A,那接下来面对的顶点和边,跟第一步从顶点 S 走到顶点 B,是完全不同的。所以,即便我们第一步选择最优的走法(边最短),但有可能因为这一步选择,导致后面每一步的选择都很糟糕,最终也就无缘全局最优解了。
2.分发糖果(Leetcode题目)
老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。
你需要按照以下要求,帮助老师给这些孩子分发糖果:
每个孩子至少分配到 1 个糖果。
相邻的孩子中,评分高的孩子必须获得更多的糖果。
那么这样下来,老师至少需要准备多少颗糖果呢?
示例 1:
输入: [1,0,2]
输出: 5
解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。
示例 2:
输入: [1,2,2]
输出: 4
解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这已满足上述两个条件。
规则定义: 设学生 AA 和学生 BB 左右相邻,AA 在 BB 左边;
左规则: 当 ratings_B>ratings_Aratings
B
ratings
A
时,BB 的糖比 AA 的糖数量多。
右规则: 当 ratings_A>ratings_Bratings
A
ratings
B
时,AA 的糖比 BB 的糖数量多。
相邻的学生中,评分高的学生必须获得更多的糖果 等价于 所有学生满足左规则且满足右规则。
算法流程:
先从左至右遍历学生成绩 ratings,按照以下规则给糖,并记录在 left 中:
先给所有学生 11 颗糖;
若 ratings_i>ratings_{i-1}ratings
i
ratings
i−1
,则第 ii 名学生糖比第 i - 1i−1 名学生多 11 个。
若 ratings_i<=ratings_{i-1}ratings
i
<=ratings
i−1
,则第 ii 名学生糖数量不变。(交由从右向左遍历时处理。)
经过此规则分配后,可以保证所有学生糖数量 满足左规则 。
同理,在此规则下从右至左遍历学生成绩并记录在 right 中,可以保证所有学生糖数量 满足右规则 。
最终,取以上 22 轮遍历 left 和 right 对应学生糖果数的 最大值 ,这样则 同时满足左规则和右规则 ,即得到每个同学的最少糖果数量。
复杂度分析:
时间复杂度 O(N)O(N) : 遍历两遍数组即可得到结果;
空间复杂度 O(N)O(N) : 需要借用left,right的线性额外空间。
c++:
class Solution {
public:
int candy(vector<int>& ratings) {
int res=ratings.size();
vector<int> tmp(res,0);
for(int i=1;i<res;i++)
if(ratings[i]>ratings[i-1])
tmp[i]=tmp[i-1]+1;
for(int i=res-1;i>0;i--)
if(ratings[i-1]>ratings[i] && tmp[i-1]<tmp[i]+1)
tmp[i-1]=tmp[i]+1;
for(int i=0;i<ratings.size();i++)
res+=tmp[i];
return res;
}
};
解释:大概就是先每个孩子发一颗糖果,然后遍历左规则和右规则就可以得到答案
3. 钱币找零(有面值为1的可以”考虑”贪心,没有就 DP )
这个问题在我们的日常生活中更加普遍。假设我们有 1 元、2 元、5 元、10 元、20 元、50 元、100 元这些面额的纸币,它们的张数分别是 c1、c2、c5、c10、c20、c50、c100。我们现在要用这些钱来支付 K 元,最少要用多少张硬币呢?
在生活中,我们肯定是先用面值最大的来支付,如果不够,就继续用更小一点面值的,以此类推,最后剩下的用 1 元来补齐。
在贡献相同期望值(纸币数目)的情况下,我们希望多贡献点金额,这样就可以让纸币数更少,这就是一种贪心算法的解决思路。直觉告诉我们,这种处理方法就是最好的。实际上,要严谨地证明这种贪心算法的正确性,需要比较复杂的、有技巧的数学推导,我不建议你花太多时间在上面,不过如果感兴趣的话,可以自己去研究下。
问题:
要求:给定面额为1,5,10,50,100,500这六种面额的硬币,各3,2,1,3,0,2枚,现在用这些硬币支付A元,求使用最少的硬币。
C++:
#include<cstdio>
using namespace std;
int solve(int A);
const int v[6] = {1,5,10,50,100,500};//面额
int main()
{
solve(620);
return 0;
}
int solve(int A)
{
int sum = 0;
int c[6] = {3,2,1,3,0,2};//每种硬币的枚数
for(int i = 0 ; i<6 ; i++) //判断所有硬币的总额
sum += v[i]*c[i];
if(sum < A)
{
printf("总额不够");
return 0;
}
int temp,index,count = 0;
while(A != 0)
{
int min = 1000000;
for(int i = 0 ; i<6 ; i++)
{
if(A/v[i]<min&&A/v[i]>0&&c[i]>0)//Min表示枚数
{
min = A/v[i];//这儿有个问题,如果枚数大于剩余的枚数,下面的c[index]就成负数了,减多了
temp = v[i];
index = i;
}
}
count+=min;
c[index]-=min;
A = A-min*temp;
printf("%d\t",temp);
if(c[index]<0) //把上面减多的加回来
{
A += temp*(-c[index]);
count+=c[index];
}
}
printf("count:%d",count);
return 0;
}





