1.什么是搜索(算法)?
搜索算法是利用计算机的高性能来有目的的穷举一个问题的部分或所有的可能情况,从而求出问题的解的一种方法。搜索过程实际上是根据初始条件和扩展规则构造一棵解答树并寻找符合目标状态的节点的过程。
给一个实例来了解这两种算法:
2.深度优先搜索(DFS)
一般形容深度搜索就是不撞南墙不回头,这个形容算非常贴切了,因为它相当于按照一定的顺序不断地走,直到走到终点位置,然后形成一种解,判断这种解符不符合我们题目的最优解。
那我们如何实现呢?首先,我们先规定它走的顺序,我们先让他向下,直到撞墙不能再向下的时候改变方向,我们用递归实现
1.什么是搜索(算法)?
搜索算法是利用计算机的高性能来有目的的穷举一个问题的部分或所有的可能情况,从而求出问题的解的一种方法。搜索过程实际上是根据初始条件和扩展规则构造一棵解答树并寻找符合目标状态的节点的过程。
给一个实例来了解这两种算法:
2.深度优先搜索(DFS)
一般形容深度搜索就是不撞南墙不回头,这个形容算非常贴切了,因为它相当于按照一定的顺序不断地走,直到走到终点位置,然后形成一种解,判断这种解符不符合我们题目的最优解。
那我们如何实现呢?首先,我们先规定它走的顺序,我们先让他向下,直到撞墙不能再向下的时候改变方向,我们用递归实现
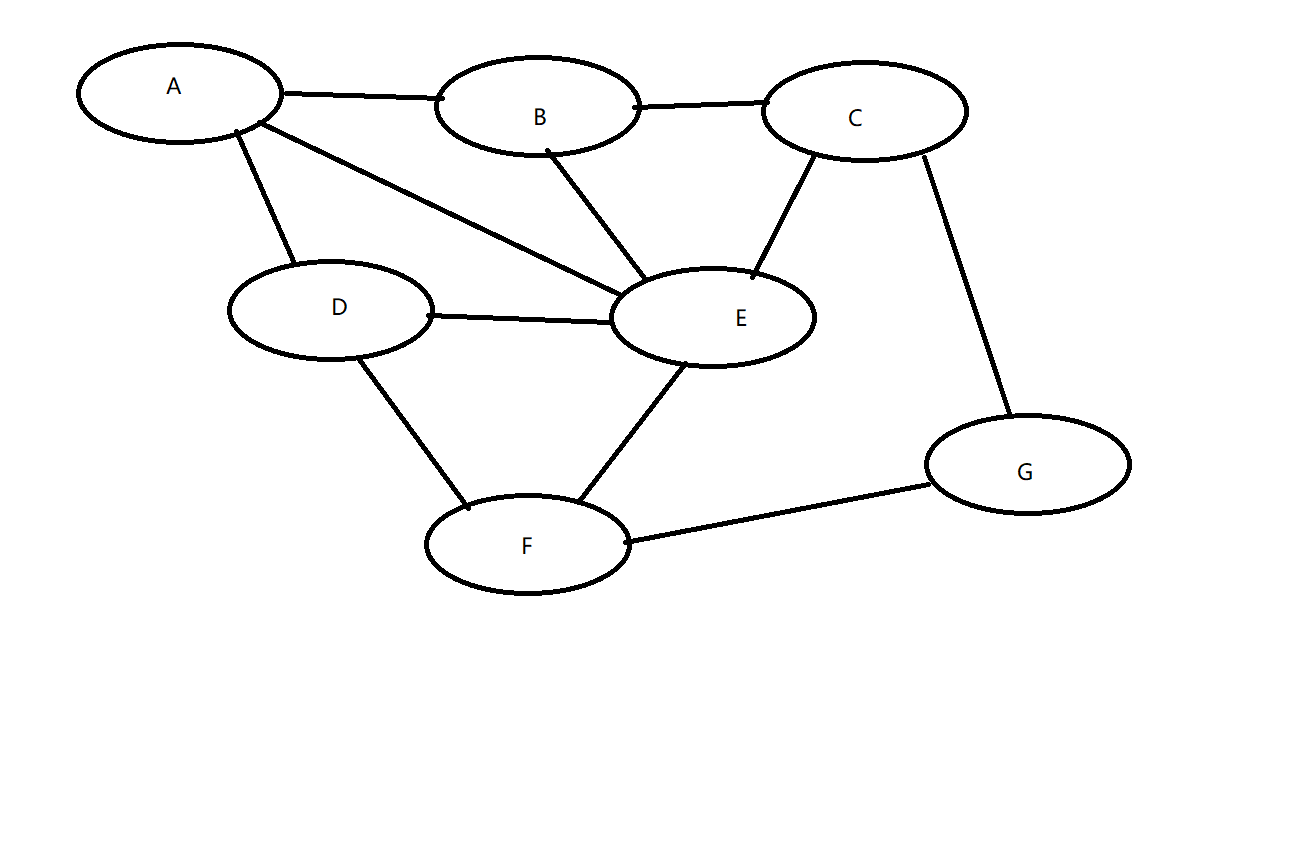
这种情况我们就可以有多种选择从A走出。而我们又不知道该怎么走才能到达G点,那么我们选择一直走我们没走过的路,这样就有可能到达G。
比如,我们可以从A到达B,C,D三个点,这是我们选择E点。
当我们从A走到E后,又可以到B,C,D,F四个点,于是我们走到B点。
当我们到达B过后,发现有三条路,分别指向A,C,E三点。
因为我们不走回头路!所以只能走到C点。
当我们走到C过后,有通往B,E,G的三个点的路,我们就可以直接走到G点了。
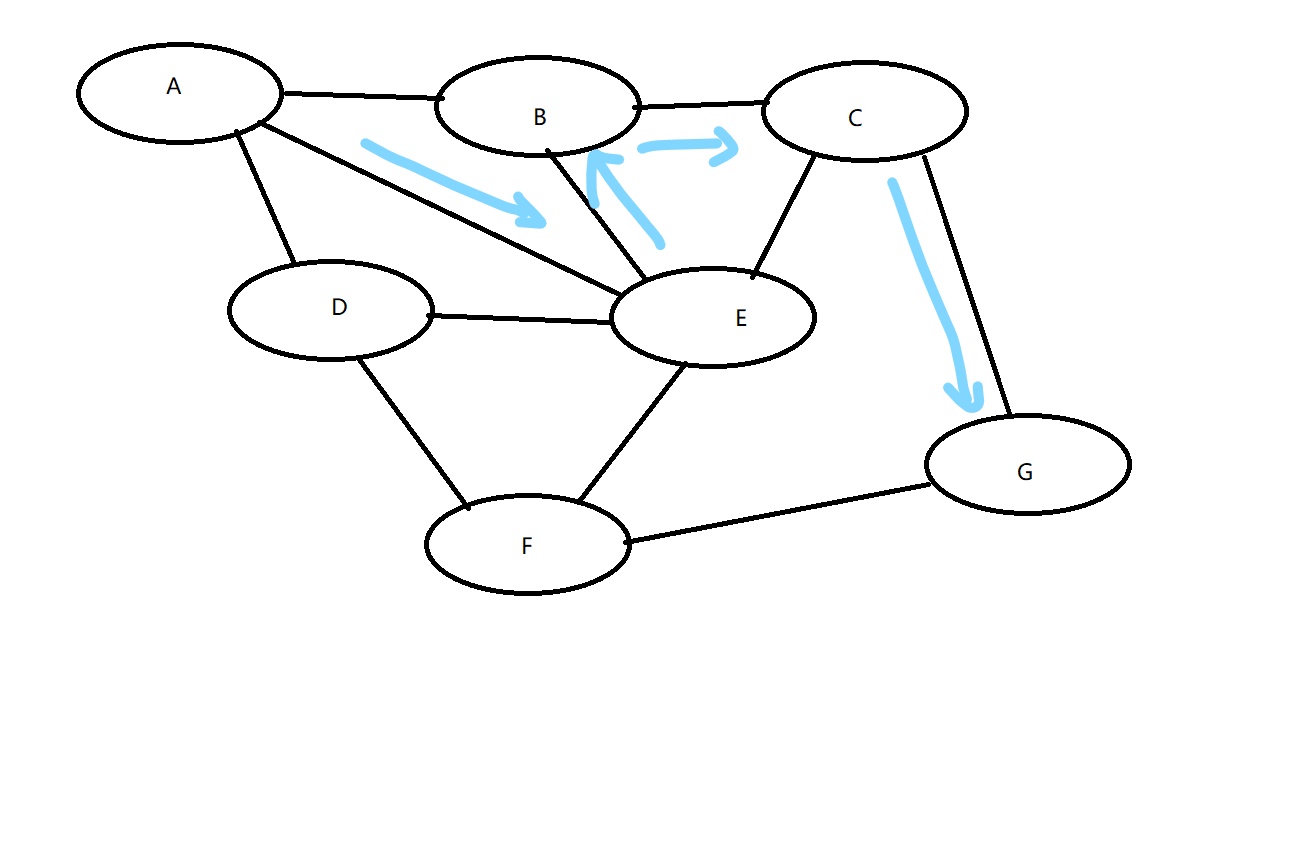
下面是深搜思路:
1.把所有点标记为“未走过”;//把数组全标记为0或者其他
2.找到起点,终点并看看可以走到哪里;//准备循环
3.选择一节点并判断本节点是否走出地图;//
4.判断这一节点走过没啊;//3、4两步是判断走到该节点是否合法
5.如果没走过就走进该节点;//标记该节点
6.再寻找下一个节点;//深入下一层搜索
7.走到头了就可以回头了//得到返回这就可以回溯了
模板:
#include <iostream>
#include <cstdio>
using namespace std;
void dfs(/*起始坐标*/){
if(/*找到出口*/){
//操作
return ;
}
for(/*循环遍历所有方向*/){
if(/*新的坐标不符合条件*/)
continue;
//操作
dfs(/*继续向下搜索新的坐标*/);
//回溯
}
}
int main(){
//读入数据
dfs(/*起点坐标*/);
return 0;
}
help庞学姐:
#include<stdio.h>
int n,m;
char mp[51][51];
int vis[51][51];
int dx[]={-1,1,0,0},dy[]={0,0,1,-1};
int ans=0,step=0,min=999999;
void dfs(int x,int y,int step){
if(x<0||x>=n||y<0||y>m) return ;
if(x==n-1&&y==m-1){ans=1;
if(step<min) min=step;
return ;}
for(int i=0;i<4;i++){
int nowx=x+dx[i];
int nowy=y+dy[i];
if(mp[nowx][nowy]=='*'&&vis[nowx][nowy]==0){
vis[nowx][nowy]=1;
dfs(nowx,nowy,step+1);
vis[nowx][nowy]=0;
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++)
scanf("%s",mp[i]);
dfs(0,0,0);
printf("%d",min);
return 0;
}
其实这里的代码看上去好像很复杂很繁琐,但是只要仔细一想,就可以看懂,深度搜索就是把所有的路都走一遍然后最短的路程就出来了,控制比如第一步
通过一个个的搜索和条件约束就可以使算法按我们的意图运行
3.广度优先搜索(BFS)
广度优先搜索算法(Breadth-First Search,BFS)是一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。BFS并不使用经验法则算法。
广度优先搜索让你能够找出两样东西之间的最短距离,不过最短距离的含义有很多!
假设你经营着一个芒果农场,需要寻找芒果销售商,以便将芒果卖给他。在Facebook,你与芒果销售商有联系吗?为此,你可在朋友中查找。

这种查找很简单。首先,创建一个朋友名单

然后,依次检查名单中的每一个人,看看他是否是芒果销售商。

重点
假设你没有朋友是芒果销售商,那么你就必须在朋友的朋友中查找。

在这个过程中就要用到队列的思想
先从你开始,关系表为下图

先概述一下这种算法的工作原理。

但这样可能会出现一些问题,Peggy既是Alice的朋友又是Bob的朋友,因此她将被加入队列两次:一次是在添加Alice的朋友时,另一次是在添加Bob的朋友时。因此,搜索队列将包含两个Peggy。

但你只需检查Peggy一次,看她是不是芒果销售商。如果你检查两次,就做了无用功。因此,检查完一个人后,应将其标记为已检查,且不再检查他。
如果不这样做,就可能会导致无限循环。假设你的人际关系网类似于下面这样。
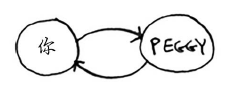
检查一个人之前,要确认之前没检查过他,这很重要。为此,你可使用一个列表来记录检查过的人。
首先,需要使用代码来实现图。图由多个节点组成。
每个节点都与邻近节点相连,如果表示类似于“你→Bob”这样的关系呢?好在你知道的一种结构让你能够表示这种关系,它就是散列表!
记住,散列表让你能够将键映射到值。在这里,你要将节点映射到其所有邻居。
引用 https://blog.csdn.net/qq_37482202/article/details/89513877
依然用help庞小姐作为例子
这道题的广度搜索源代码:
#include<bits/stdc++.h>
using namespace std;
int n,m;
struct node {
int x,y,step;
node(int _a,int _b,int _c){x=_a,y=_b,step=_c;}
};
string mp[57];
int vis[57][57];
int dx[]={-1,1,0,0};
int dy[]={0,0,-1,1};
int bfs()
{
queue<node> q;
q.push(node(0,0,0));
while(!q.empty()){
node f=q.front();
q.pop();
for(int i=0;i<4;i++){
int nowx=f.x+dx[i];
int nowy=f.y+dy[i];
if(nowx<0||nowy<0||nowx>=n||nowy>=m)
continue;
if(nowx==n-1&&nowy==m-1)
return f.step+1;
if(mp[nowx][nowy]=='*'&&vis[nowx][nowy]==0)
{
q.push(node(nowx,nowy,f.step+1));
vis[nowx][nowy]=1;
}
}
}
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++) cin>>mp[i];
cout<<bfs();
return 0;
}
可能有人也看出来了,为什么这里的算法不需要像深度搜索那样,整个min,就可以得到最小值了呢?
这是因为每一步都打上了标记,每一步都是基于前面的尝试得到的最优解,所以不存在去考虑什么最优解,这也是广度搜索比深度搜索好的方面,在实际运行时可以极大的缩减时间,但是占用内存较大,深度搜索刚刚好反过来。
有时候面对题目的时候真的觉得深度搜索的局限性太高了,比如求x->y的时候,用深度搜索真的不如广度搜索,比如求2->37结果是6,但是广度搜索就是一直走下去,如果你拟规定的边界不太好的话,可能还输出不了
但是,广度搜索真的比较好用,他会挨个挨个寻找,这样比较好,他的挨个挨个找并不是毫无根据的,他通过一些关系紧密联系在一起的规律找。
下面的内容比较深奥,建议好好掌握上面的再来掌握下面的(更新中)





